NANOSYSTEMS: PHYSICS, CHEMISTRY, MATHEMATICS, 2020, 11 (1), P. 5–13
A mathematical study of the flow of nanoparticles inside periodic permeable and viscoelastic lung
Jyoti Kori – Department of Mathematics, Indian Institute of Technology Roorkee, Roorkee-247667, Uttarakhand, India; jyotikorii@gmail.com
Pratibha – Department of Mathematics, Indian Institute of Technology Roorkee, Roorkee-247667, Uttarakhand, India
Mohammad Junaid Abbasi – Department of Mathematics, Indian Institute of Technology Roorkee, Roorkee-247667, Uttarakhand, India
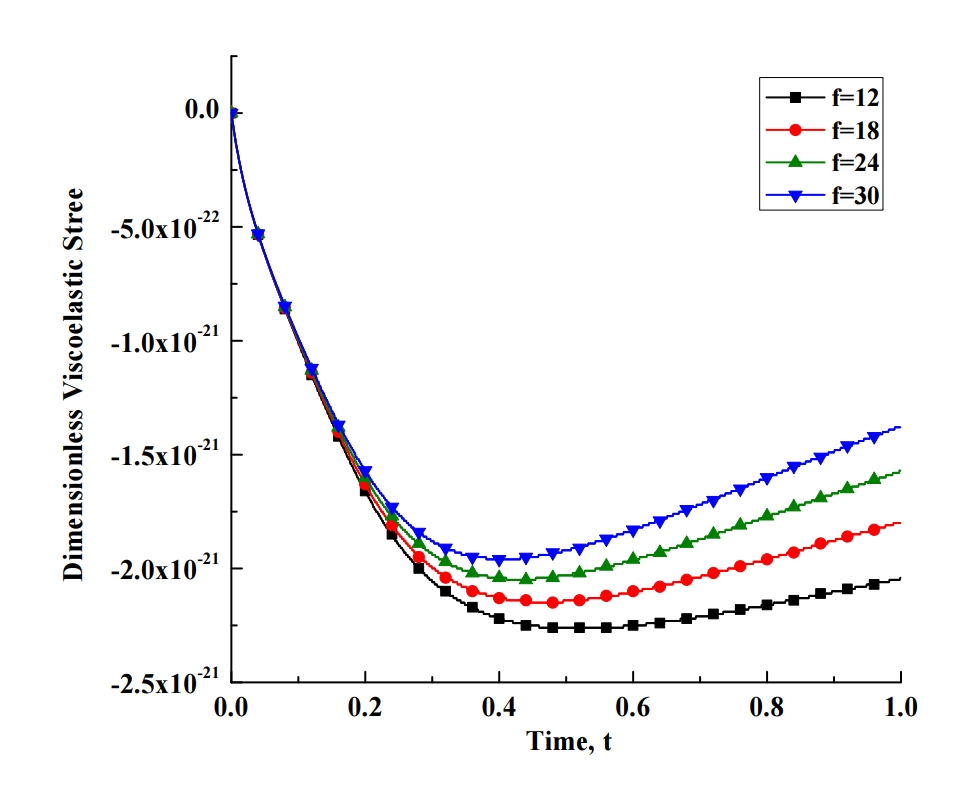
Smoking and pollution are highly hazardous to human health. Most of the environmental particles are very small in size i.e. micro or nanoparticles. When these particles are inhaled, they enter from the nose and flow with the air stream into various portions of the lungs. The alveolar region, a porous media due to number of alveoli, serves as an internal biofilter medium to filter deposited particles. To analyze the behavior of this biofilter medium, we considered the periodic permeability of lungs (due to periodic breathing) together with the viscoelasticity of the lung tissues. The flow of viscous air through the porous media is modeled by using one dimensional momentum equation with Darcy’s law and the velocity of particles by second law of Newton. To model the viscoelasticity, we used Kelvin-Voigt model. The finite difference method is used to solve the governing equations and MATLAB is used to solve the computational problem. The effects of various parameters, such as the Darcy number, porosity, and the breathing frequency are analyzed for flow of air, particle and viscoelasticity of lung graphically. Results show that by increasing the breathing frequency, decreasing the porosity, and decreasing the Darcy number, the viscoelastic stress increases.
Keywords: Breathing frequency, Darcy number, lungs tissue, periodic permeability, porous media, viscoelasticity.
DOI 10.17586/2220-8054-2020-11-1-5-13