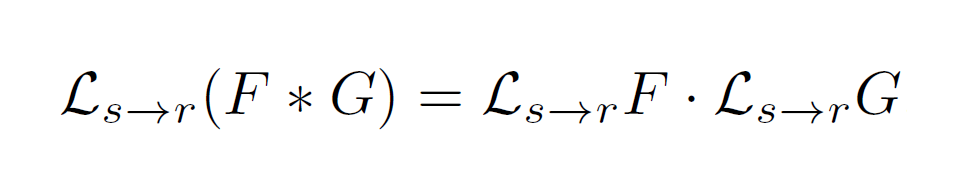NANOSYSTEMS: PHYSICS, CHEMISTRY, MATHEMATICS, 2021, 12 (1), P. 15–21
Discrete spectrum Analysis using Laplace transform and Volterra equations (DALV-method)
V.V. Kuidin – ITMO University, St. Petersburg 197101, Russia; vladislav.kujdin@metalab.ifmo.ru
V.V. Zalipaev – ITMO University, St. Petersburg 197101, Russia
D. R. Gulevich – ITMO University, St. Petersburg 197101, Russia
The theory of excitons in two dimensional materials including graphene and transition metal dichalcogenides (TMD) is complicated, as there appears a screened interaction in equations. Such interaction can be represented as Keldysh potential. The exact solution does not seem to exist yet. The method of searching appropriate solutions to equations of quantum mechanics is believed to solve this problem by using Laplace transform of tempered distributions and Volterra equations. The method is to seek solution as a Laplace transform of some tempered distribution that satisfies the appropriate Laplace spectral equation which, under Laplace transform, gives us the initial equation. Due to Paly–Wigner–Schwarz theorem, the image functions behavior depends on the geometry of original one support. In addition, the homogenous Volterra equation does not have nontrivial continuous solution. These constraints together with the fact that the studied equations turn out to be Volterra equations of III kind lead to a method that seems to solve a wide class of quantum mechanics equations.
Keywords: discrete spectrum, Laplace transform, Volterra equation, Schrödinger equation.
PACS 02.70.Hm, 02.30.Hq, 03.65.Ge
DOI 10.17586/2220-8054-2021-12-1-15-21
[In Russian] В.В. Куйдин, В.В. Залипаев, Д. Р. Гулевич
Анализ дискретного спектра с использованием преобразования Лапласа и уравнений Вольтерра (DALV-метод)
Теория экситонов в двумерных материалах, включая графен и дихалькогениды переходных металлов (ДМД), сложна, так как в уравнениях появляется экранированное взаимодействие. Такое взаимодействие можно представить как потенциал Келдыша. Точного решения пока не существует. Считается, что метод поиска подходящих решений уравнений квантовой механики решает эту проблему с использованием преобразования Лапласа, обобщенных функций и уравнений Вольтерра. Метод заключается в поиске решения в виде преобразования Лапласа некоторой обобщенной функции, которая удовлетворяет соответствующему спектральному уравнению Лапласа, которое при преобразовании Лапласа дает нам исходное уравнение. По теореме Пэли–Винера–Шварца поведение образов функций зависит от геометрии носителя исходной функции. Кроме того, однородное уравнение Вольтерра не имеет нетривиального непрерывного решения. Эти ограничения вместе с тем, что изучаемые уравнения оказываются уравнениями Вольтерра III рода, приводят к методу, который, по-видимому, решает широкий класс уравнений квантовой механики.
Ключевые слова: дискретный спектр, преобразование Лапласа, уравнение Вольтерра, уравнение Шредингера.