NANOSYSTEMS: PHYSICS, CHEMISTRY, MATHEMATICS, 2021, 12 (1), P. 42–59
Domain wall evolution at nanowires in terms of 3D LLG equation initial-boundary problem
S. Leble – Immanuel Kant Baltic Federal University, 236041 Kaliningrad, Russia; lebleu@mail.ru
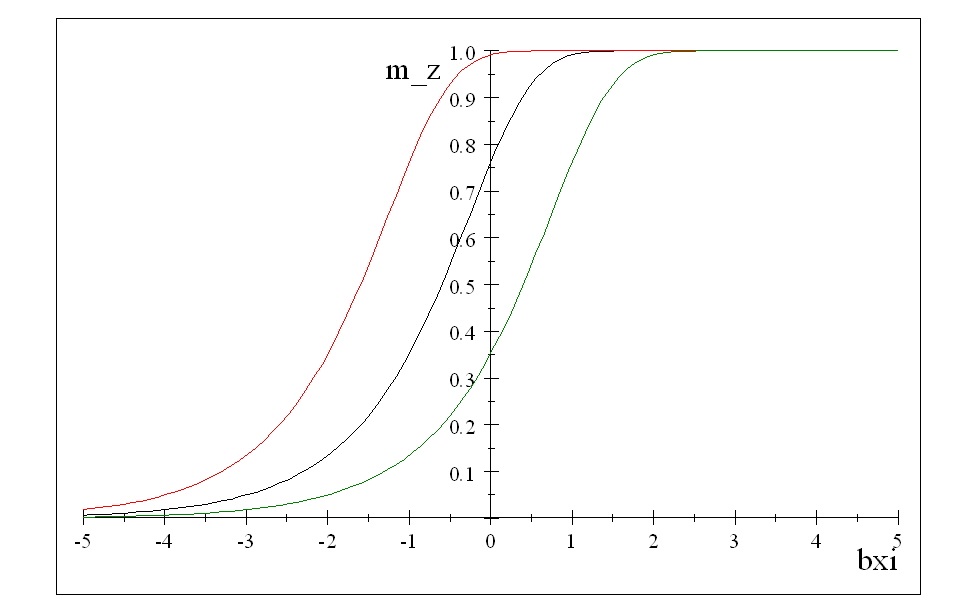
A theory of a domain wall creation and propagation is built on a linearized version of the transformed Landau–Lifshitz–Gilbert equation. The Lakshmanan–Nakamura stereo-graphic transform, after extra exponential transformation, and, next – linerization partially save information of the original nonlinearity that allows one to keep the domain wall dynamics, form and properties. For cylindrical-symmetric wire geometry, the conventional orthonormal Bessel basis, combined with projecting operators technique applied to subspaces of directed propagation of domain walls is constructed. The physically significant problems of the dynamics switching at points far and close from a wire ends are formulated and its solutions are presented in the frame of the Fourier method. Stationary solutions are found and the wall structure along the wire and propagation plots are drawn.
Keywords: Nanowire magnetization dynamics, domain wall creation, Landau–Lifshitz–Gilbert equation, Lakshmanan–Nakamura transform,
initial-boundary problem.
PACS 75.70.Cn, 05.30.d, 02.20.a
DOI 10.17586/2220-8054-2021-12-1-42-59
[In Russian] С. Лебле
Эволюция границ доменов в нанопроводах в терминах гранично-начальной задачи для 3D LLG уравнения
Теория образования и распространения доменных стенок построена на линеаризованной версии преобразованного уравнения Ландау–Лифшица–Гилберта. Стереографическое преобразование Лакшманана–Накамуры после дополнительного экспоненциального преобразования, а затем линеаризации частично сохраняет информацию об исходной нелинейности, что позволяет сохранить динамику, форму и свойства доменной стенки. Для цилиндрически-симметричной геометрии провода построен традиционный ортонормированный базис Бесселя в сочетании с техникой проекционных операторов, применяемой к подпространствам направленного распространения доменных стенок. Сформулированы физически значимые задачи переключения динамики в дальних и близких точках от концов провода и представлены их решения в рамках метода Фурье. Находятся стационарные решения и вычерчиваются структура стены вдоль провода и участки распространения.
Ключевые слова: динамика намагниченности нанопроводов, создание доменных стенок, уравнение Ландау–Лифшица–Гильберта, преобразование Лакшманана–Накамуры, начально-краевая задача