Nanosystems: Phys. Chem. Math., 2022, 13 (2), 156–163.
On the discrete spectrum of a quantum waveguide with Neumann windows in presence of exterior field
A. S. Bagmutov – ITMO University, St. Petersburg, 197101, Russia; bagmutov94@mail.ru
H. Najar – Departement de Mathematiques, Faculte des Sciences de Moanstir. Avenue de l’environnement 5019 Monastir, Tunisie; hatemnajar@ipeim.rnu.tn
I. F. Melikhov – ITMO University, St. Petersburg, 197101, Russia; ivan.melikhov@gmail.com
I. Y. Popov – ITMO University, St. Petersburg, 197101, Russia; popov1955@gmail.com
Corresponding author: A. S. Bagmutov, bagmutov94@mail.ru
DOI 10.17586/2220-8054-2022-13-2-156-163
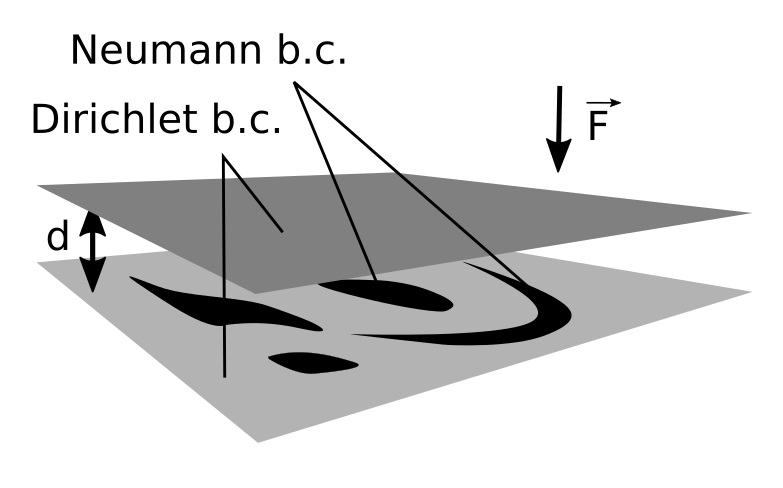
ABSTRACT The discrete spectrum of the Hamiltonian describing a quantum particle living in three dimensional straight layer of width d in the presence of a constant electric field of strength F is studied. The Neumann boundary conditions are imposed on a finite set of bounded domains (windows) posed at one of the boundary planes and the Dirichlet boundary conditions on the remaining part of the boundary (it is a reduced problem for two identical coupled layers with symmetric electric field). It is proved that such system has eigenvalues below
the lower bound of the essential spectrum for any F≥0. Then we closer examine a dependence of bound state energies on F and window’s parameters, using numerical methods.
KEYWORDS quantum waveguide, Schrödinger operator, discrete spectrum.
ACKNOWLEDGEMENTS The work was partially supported by grant 20-31-90050 of Russian Foundation for Basic Research.
FOR CITATION Bagmutov A.S., Najar H., Melikhov I.F., Popov I.Y. On the discrete spectrum of a quantum waveguide with Neumann windows in presence of exterior field. Nanosystems: Phys. Chem. Math., 2022, 13 (2), 156–163.
[In Russian] А.С. Багмутов, Х. Наджар, И.Ф. Мелихов, И.Ю. Попов
О дискретном спектре квантового волновода с неймановскими окнами при наличии внешнего поля
АННОТАЦИЯ Исследован дискретный спектр гамильтониана, описывающего квантовую частицу, живущую в трехмерном прямолинейном слое шириной d в присутствии постоянного электрического поля напряженностью F. Граничные условия Неймана накладываются на конечное множество ограниченных областей (окон), находящихся на одной из граничных плоскостей, а граничные условия Дирихле — на оставшейся части границы (это редуцированная задача для двух одинаковых связанных слоев с симметричным электрическим полем). Доказано, что такая система имеет собственные значения ниже нижней границы существенного спектра для любого F≥0. Затем мы более подробно исследуем зависимость энергий связанных состояний от F и параметров окна, используя численные методы.
КЛЮЧЕВЫЕ СЛОВА квантовый волновод, оператор Шредингера, дискретный спектр.