Nanosystems: Phys. Chem. Math., 2022, 13 (3), 299–307
Ladder operators approach to representation classification problem for Jordan–Schwinger image of su(2) algebra
Gleb V. Tushavin – ITMO University, Saint Petersburg, Russia
Alexander I. Trifanov – ITMO University, Saint Petersburg, Russia
Ekaterina V. Zaitseva – ITMO University, Saint Petersburg, Russia
Corresponding author: Gleb V. Tushavin, gleb@tushavin.ru
DOI 10.17586/2220-8054-2022-13-3-299-307
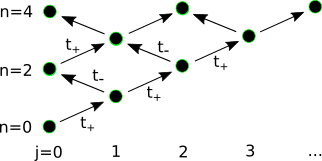
ABSTRACT The eigenvalues of the complete commuting set of self-adjoint operators determine the classification of states. We construct a classification for the image of the Jordan–Schwinger mapping of the su(2) algebra. We use the ladder operator approach to construct a canonical basis of irreducible representations and define the self-adjoint operators of the complete commuting set.
KEYWORDS Ladder operators, su(2), Jordan–Schwinger map, representation theory
FOR CITATION Tushavin G.V., Zaitseva E.V., Trifanov A.I. Ladder operators approach to representation classification problem for Jordan–Schwinger image of su(2) algebra. Nanosystems: Phys. Chem. Math., 2022, 13 (3), 299–307.
[In Russian] Г.В. Тушавин, А.И. Трифанов, Е.В. Зайцева
Метод лестничных операторов в задаче классификации представления образа алгебры su(2) при отображении Жордана-Швингера
АННОТАЦИЯ Собственные числа полного коммутирующего набора наблюдаемых определяют классификацию состояний. Мы решаем задачу классификации для образа алгебры su(2) при отображении Жордана-Швингера. Мы используем метод лестничных операторов для построения канонического базиса неприводимых представлений и определяем с их помощью полный коммутирующий набор.
КЛЮЧЕВЫЕ СЛОВА лестничные операторы, su(2), отображение Жордана-Швингера, теория представлений