Nanosystems: Phys. Chem. Math., 2023, 14 (1), 28–43
Exact irregular solutions to radial Schrödinger equation for the case of hydrogen-like atoms
Chander Parkash – Department Of Mathematics, Rayat Bahra University, Mohali, Punjab, 140104, India
William C. Parke – Department Of Physics, The George Washington University, Washington D.C., USA
Parvinder Singh – Department of Chemistry, Rayat Bahra University, Mohali, Punjab, 140104, India
Corresponding author: William C. Parke, wparke@email.gwe.edu
DOI 10.17586/2220-8054-2023-14-1-28-43
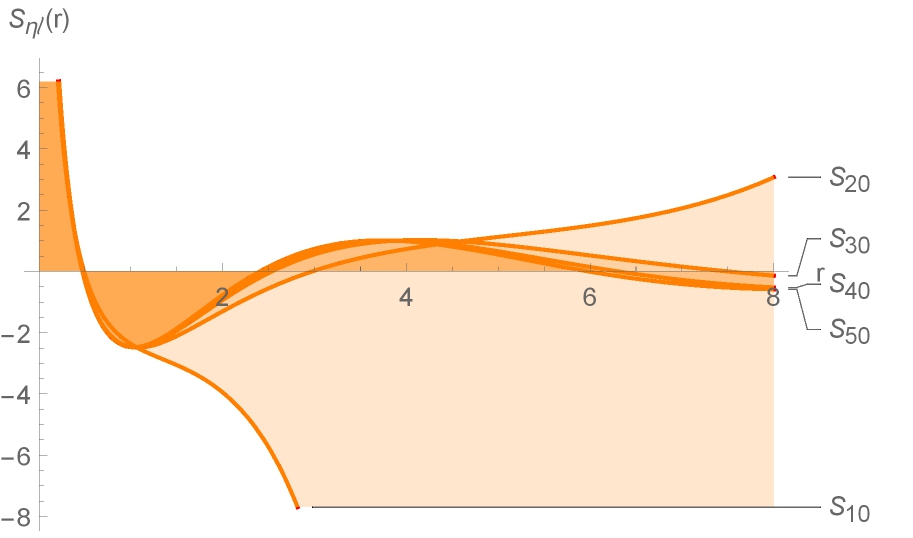
ABSTRACT This study propounds a novel methodology for obtaining the explicit/closed representation of the two linearly independent solutions of a large class of second order ordinary linear differential equation with special polynomial coefficients. The proposed approach is applied for obtaining the closed forms of regular and irregular solutions of the Coulombic Schrödinger equation for an electron experiencing the Coulomb force, and examples are displayed. The methodology is totally distinguished from getting these solutions either by means of associated Laguerre polynomials or confluent hypergeometric functions. Analytically, both the regular and irregular solutions spread in their radial distributions as the system energy increases from strongly negative values to values closer to zero. The threshold and asymptotic behavior indicate that the regular solutions have an rl dependence near the origin, while the irregular solutions diverge as r-l-1. Also, the regular solutions drop exponentially in proportion to rn-1exp(-r/n), in natural units, while the irregular solutions grow as r-n-1exp(r/n). Knowing the closed form irregular solutions leads to study the analytic continuation of the complex energies, complex angular momentum, and solutions needed for studying bound state poles and Regge trajectories.
KEYWORDS second exact solutions, irregular exact solutions, Coulombic Schrödinger equation, Frobenius method, Coulombic interaction
ACKNOWLEDGEMENTS The authors are grateful to Prof. Nyengeri Hippolyte, Department of Physics, Faculty of Science, University of Burundi, Bujumbura, Burundi, for providing his contribution towards the finalization of this manuscript.
FOR CITATION Parkash C, Parke W.C., Singh P. Exact irregular solutions to radial Schrödinger equation for the case of hydrogen-like atoms. Nanosystems: Phys. Chem. Math., 2023, 14 (1), 28–43.
[In Russian] Чандер Паркаш, Уильям С. Парк, Парвиндер Сингх
Точные нерегулярные решения радиального уравнения Шрёдингера для случая водородоподобных атомов
АННОТАЦИЯ В этом исследовании предлагается новая методология получения явного замкнутого представления двух линейно независимых решений большого класса обыкновенных линейных дифференциальных уравнений второго порядка со специальными полиномиальными коэффициентами. Предложенный подход применяется для получения замкнутых форм регулярных и нерегулярных решений кулоновского уравнения Шредингера для электрона, находящегося под действием кулоновской силы, и приводятся примеры. Методология отличается от основанной на использовании полиномов Лагерра или вырожденных гипергеометрических функций. Радиальное распределение аналитических, как регулярных, так и нерегулярных, решений размывается по мере увеличения энергии системы от сильно отрицательных значений до значений, близких к нулю. Порог и асимптотика показывают, что регулярные решения имеют зависимость rl вблизи начала координат, а нерегулярные решения расходятся как r-l-1. Кроме того, обычные решения cпадают экспоненциально пропорционально rn-1exp(-r/n), в естественных единицах, а нерегулярные решения растут как r-n-1exp(r/n). Знание нерегулярных решений в замкнутой форме приводит к изучению аналитического продолжения в область комплексных энергий, комплексного углового момента и решений, необходимых для изучения полюсов связанного состояния и траекторий Редже.
КЛЮЧЕВЫЕ СЛОВА вторые точные решения, нерегулярные точные решения, кулоновское уравнение Шредингера, метод Фробениуса, кулоновское взаимодействие.