Nanosystems: Phys. Chem. Math., 2024, 15 (5), 586–596
Inverse source problem for the subdiffusion equation with edge-dependent order of time-fractional derivative on the metric star graph
Zarifboy A. Sobirov – National University of Uzbekistan, 100174, Tashkent; V. I. Romanovskiy Institute of Mathematics, Uzbekistan Academy of Science, 100174, Tashkent, Uzbekistan; z.sobirov@nuu.uz
Ariukhan A. Turemuratova – National University of Uzbekistan, 100174, Tashkent; Branch of Russian Economic University named after G. V. Plekhanov in Tashkent, 100164, Tashkent, Uzbekistan; ariuxanturemuratova@gmail.com
Corresponding author: Z. A. Sobirov, z.sobirov@nuu.uz
PACS 02.30.Jr, 02.30.Zz
DOI 10.17586/2220-8054-2024-15-5-586-596
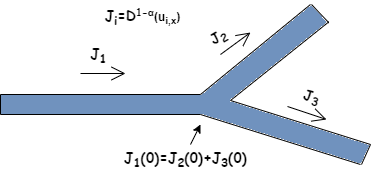
ABSTRACT The paper discusses the inverse source problem for the subdiffusion equation in the Sobolev space. The direct and inverse problems are transformed into operator equations to derive solutions. The uniqueness and existence of a strong solution to the direct problem are proven. The inverse problem is reduced to an operator equation, and the well-definedness and continuity of the corresponding resolvent operator are proven.
KEYWORDS subdiffusion equation, star metric graph, inverse problem, generalized solution, resolvent operator
FOR CITATION Sobirov Z.A., Turemuratova A.A. Inverse source problem for the subdiffusion equation with edge-dependent order of time-fractional derivative on the metric star graph. Nanosystems: Phys. Chem. Math., 2024, 15 (5), 586–596.
[In Russian] Собиров З.А., Туремуратова А.А.
Обратная задача источника для уравнения субдиффузии с зависящим от ребра порядком дробной производной по времени на метрическом звездообразном графе
АННОТАЦИЯ В статье обсуждается обратная задача источника для уравнения субдиффузии в пространстве Соболева. Для исследования разрешимости прямая и обратная задачи преобразуются в операторные уравнения. Доказаны единственность и существование сильного решения прямой задачи. Обратная задача сводится к операторному уравнению, и доказан непрерывность соответствующего оператора-резольвенты.
КЛЮЧЕВЫЕ СЛОВА уравнение субдиффузии, звездообразный метрический граф, обратная задача, обобщенное решение, резольвентный оператор.