01

NANOSYSTEMS: PHYSICS, CHEMISTRY, MATHEMATICS, 2021, 12 (6), P. 657–663

Monotonicity of the eigenvalues of the two-particle Schrödinger operatoron a lattice

J. I. Abdullaev – Institute of Mathematics of the Academy of Sciences of the Republic of Uzbekistan, Mirzo Ulugbek 81, Tashkent 100170; Samarkand State University, University Boulevard 15, Samarkand 140104, Uzbekistan; jabdullaev@mail.ru
A. M. Khalkhuzhaev – Institute of Mathematics of the Academy of Sciences of the Republic of Uzbekistan, Mirzo Ulugbek 81, Tashkent 100170; Samarkand State University, University Boulevard 15, Samarkand 140104, Uzbekistan; ahmad_x@mail.ru
L. S. Usmonov – Samarkand State University, University Boulevard 15, Samarkand 140104, Uzbekistan; u.lochinbek@bk.ru

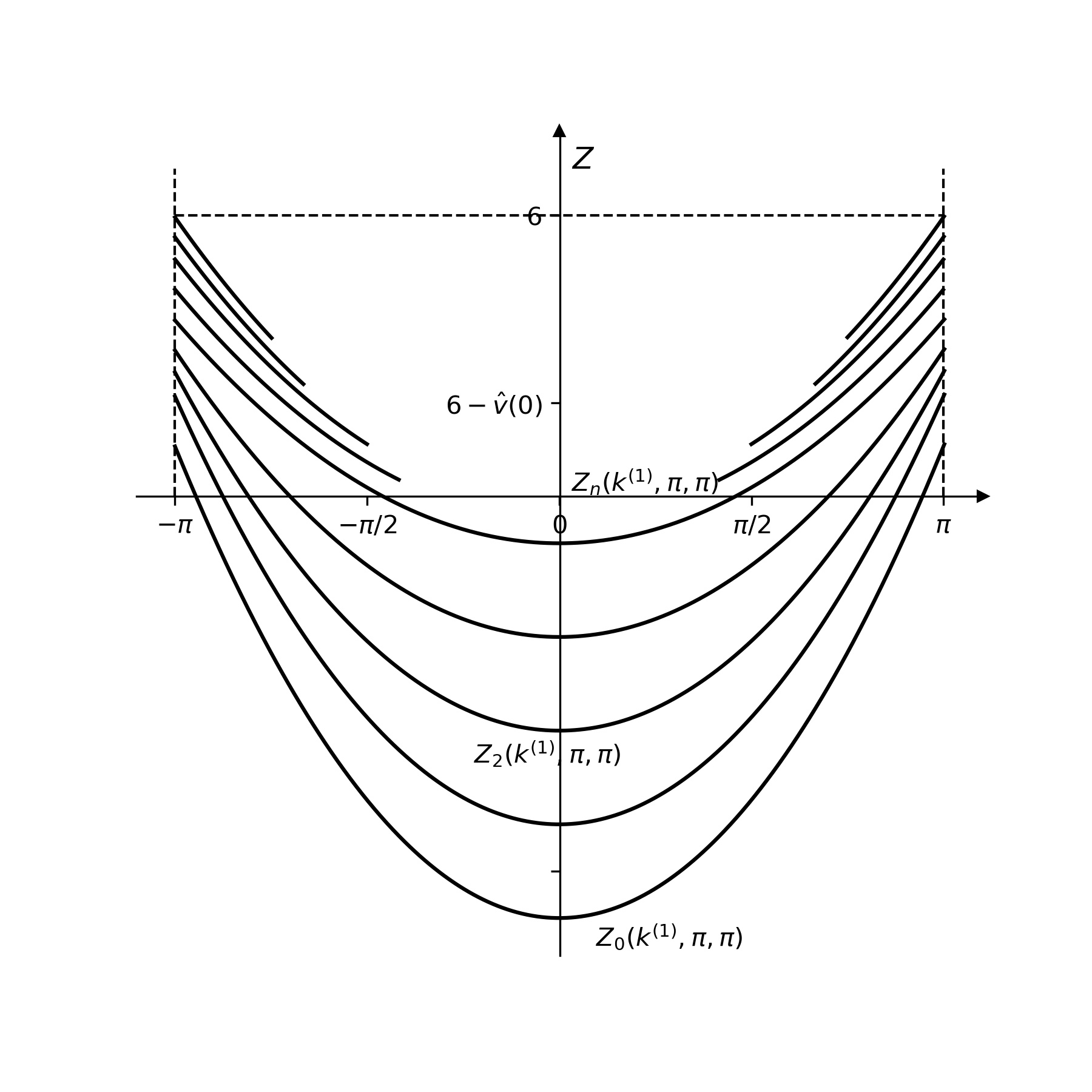
We consider the two-particle Schrödinger operator H(k), (k∈T³≡(-π, π]³ is the total quasimomentum of a system of two particles) corresponding to the Hamiltonian of the two-particle system on the three-dimensional lattice Z³. It is proved that the number N(k)≡N(k⁽¹⁾, k⁽²⁾, k⁽³⁾) of eigenvalues below the essential spectrum of the operator H(k) is nondecreasing function in each k⁽ⁱ⁾≡[0, π], i = 1, 2, 3. Under some additional conditions potential vˆ, the monotonicity of each eigenvalue z_n(k)≡z_n(k⁽¹⁾, k⁽²⁾, k⁽³⁾) of the operator H(k) in k⁽ⁱ⁾≡[0, π] with other coordinates k being fixed is proved.

Keywords: two-particle Schrödinger operator, Birman-Schwinger principle, total quasimomentum, monotonicity of the eigenvalues.

PACS 02.30.Tb

DOI 10.17586/2220-8054-2021-12-6-657-663

Download

[In Russian] Дж. И. Абдуллаев, А. М. Халхуджаев, Л. С. Усмонов

Монотонность собственных значений двухчастичного оператора Шредингера на решетке

Рассмотрим двухчастичный оператор Шредингера H(k), (k∈T³≡(-π, π]³ — полный квазиимпульс системы двух частиц), соответствующий гамильтониану двухчастичной системы на трехчастичном размерной решетке Z³. Доказано, что число N(k)≡N(k⁽¹⁾, k⁽²⁾, k⁽³⁾) собственных значений ниже существенного спектра оператора H(k) является неубывающей функцией при каждом k⁽ⁱ⁾≡[0, π], i = 1, 2, 3. При некоторых дополнительных условиях на потенциал vˆ, доказана монотонность каждого собственного значения z_n(k)≡z_n(k⁽¹⁾, k⁽²⁾, k⁽³⁾) оператора H(k) в k⁽ⁱ⁾≡[0, π] при фиксированных остальных координатах k.

Ключевые слова: двухчастичный оператор Шрёдингера, принцип Бирмана-Швингера, полный квазиимпульс, монотонность собственных значений