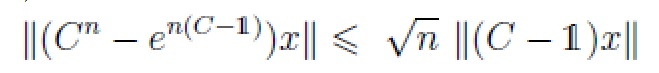Nanosystems: Phys. Chem. Math., 2022, 13 (1), 17–23
Comments on the Chernoff estimate
Valentin A. Zagrebnov – Institut de Mathématiques de Marseille, 13453 Marseille, France; Valentin.Zagrebnov@univ-amu.fr
DOI 10.17586/2220-8054-2022-13-1-17-23
PACS 02.30.Sa, 02.30.Tb
ABSTRACT The Chernoff sqrt(n)-Lemma is revised. This concerns two aspects: a re-examination of the Chernoff estimate in the strong operator topology and the operator-norm estimate for quasi-sectorial contractions. Applications to the Lie-Trotter product formula approximation C0-semigroups are also discussed.
KEYWORDS Chernoff lemma, Semigroup theory, Product formula, Convergence rate.
ACKNOWLEDGEMENTS The strong convergence with the rate (c) (see, Section 3) was established for the first time by T. Möbus and C. Rouzé in [1, Lemma 4.2] by the method, which is different to that in our Lemma 3.1. I am thankful to Tim Möbus for useful correspondences and, in particular, for attracting my attention to an inconsistency in [2, Lemma 2.1], which is corrected in the present paper. These Comments are based on my lecture delivered on the Pierre Duclos Workshop (20-22 September 2021) at National Research University ITMO, Russian Federation. I am grateful to Prof. Igor Yu. Popov for invitation.
FOR CITATION Zagrebnov V.A. Comments on the Chernoff estimate. Nanosystems: Phys. Chem. Math., 2022, 13 (1), 17–23.
[In Russian] В.А. Загребнов
Комментарии об оценке Чернова
АННОТАЦИЯ sqrt(n)-лемма Чернова изменена. Это касается двух аспектов: пересмотра оценки Чернова в сильной операторной топологии и оценки операторной нормы для квазисекторных сжатий. Также обсуждаются приложения к аппроксимации C0-полугрупп формулой произведения Ли-Троттера.
КЛЮЧЕВЫЕ СЛОВА лемма Чернова, теория полугрупп, формула произведения, скорость сходимости.