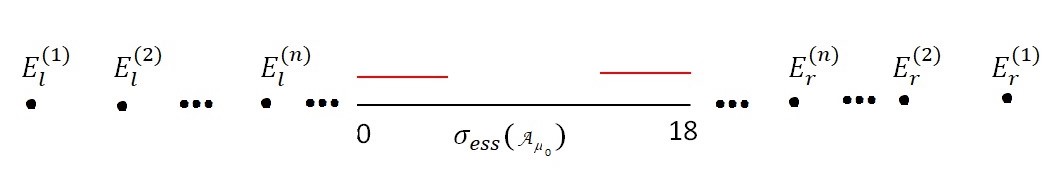NANOSYSTEMS: PHYSICS, CHEMISTRY, MATHEMATICS, 2020, 11 (2), P. 138–144
Analysis of the spectrum of a 2×2 operator matrix. Discrete spectrum asymptotics
T. H. Rasulov – Faculty of Physics and Mathematics, Bukhara State University, M. Ikbol str. 11, 200100 Bukhara, Uzbekistan; rth@mail.ru
E. B. Dilmurodov – Faculty of Physics and Mathematics, Bukhara State University, M. Ikbol str. 11, 200100 Bukhara, Uzbekistan; elyor.dilmurodov@mail.ru
We consider a 2×2 operator matrix Aμ, μ>0 related with the lattice systems describing two identical bosons and one particle, another nature in interactions, without conservation of the number of particles. We obtain an analog of the Faddeev equation and its symmetric version for the eigenfunctions of Aμ. We describe the new branches of the essential spectrum of Aμ via the spectrum of a family of generalized Friedrichs models. It is established that the essential spectrum of Aμ consists the union of at most three bounded closed intervals and their location is studied. For the critical value μ0 of the coupling constant μ we establish the existence of infinitely many eigenvalues, which are located in the both sides of the essential spectrum of Aμ. In this case, an asymptotic formula for the discrete spectrum of Aμ is found.
Keywords: operator matrix, bosonic Fock space, coupling constant, dispersion function, essential and discrete spectrum, Birman–Schwinger principle, spectral subspace, Weyl creterion.
DOI 10.17586/2220-8054-2020-11-2-138-144