NANOSYSTEMS: PHYSICS, CHEMISTRY, MATHEMATICS, 2020, 11 (3), P. 275–284
Approximate analytical method for finding eigenvalues of Sturm-Liouville problem with generalized boundary condition of the third kind
V. D. Lukyanov – Joint-Stock Company “Avangard”, Kondrat’evsky, 72, St. Petersburg, 195271, Russia; lukyanovvd@rambler.ru
D. A. Bulekbaev – Mozhaisky Military Space Academy, Zhdanovskaya, 13, St. Petersburg, 197198, Russia; atiman@mail.ru
A.V. Morozov – Mozhaisky Military Space Academy, Zhdanovskaya, 13, St. Petersburg, 197198, Russia; alex.morozof@gmail.com
L.V. Nosova – Mozhaisky Military Space Academy, Zhdanovskaya, 13, St. Petersburg, 197198, Russia; lvn1201@gmail.com
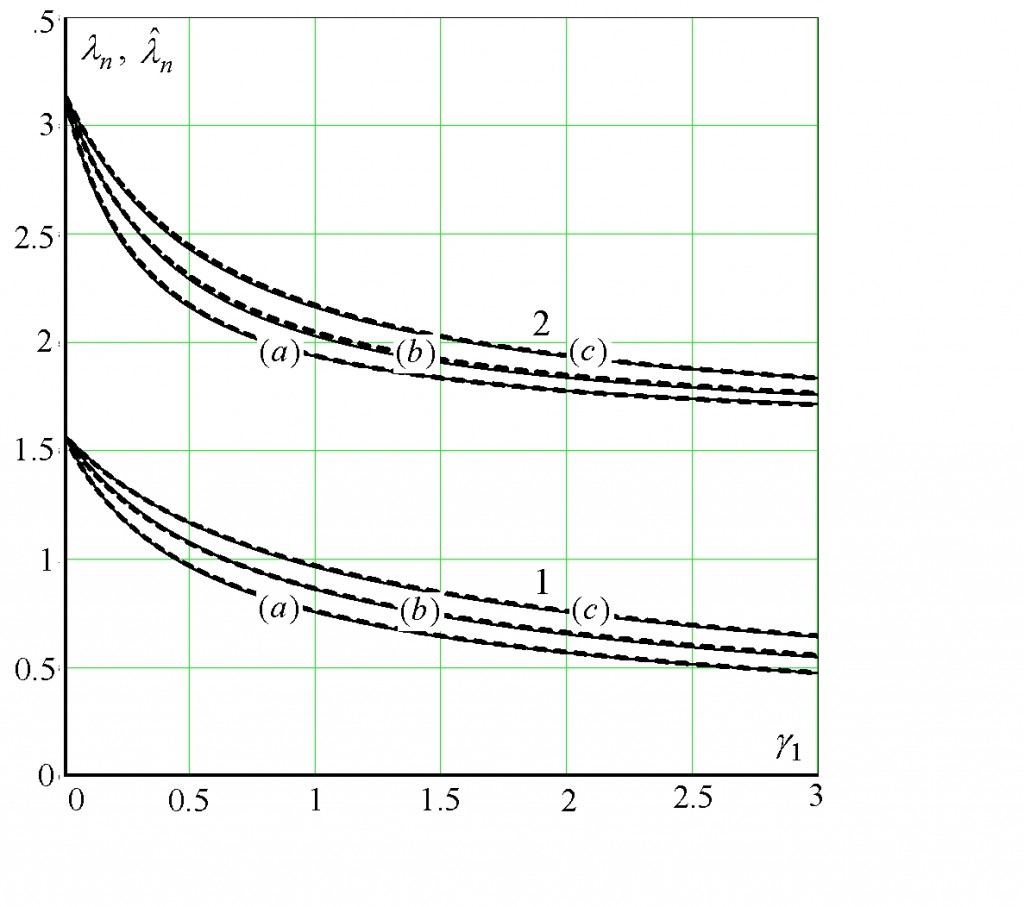
The Sturm-Liouville problem is solved for a linear differential second-order equation with generalized boundary conditions of the third kind Generalized boundary conditions consist of a linear combination of the boundary values of a function and its derivative. The coefficients of the linear combination are polynomials of the boundary problem eigenvalue. A method of approximate analytical calculation of boundary problem eigenvalues is proposed The calculation error of an eigenvalue is estimated.
Keywords: Sturm-Liouville problem, boundary conditions of the third kind, eigenfunctions, eigenvalues, approximation.
PACS 02.60.Lj, 47.61.Fg, 62.25.-g
DOI 10.17586/2220-8054-2020-11-3-275-284