NANOSYSTEMS: PHYSICS, CHEMISTRY, MATHEMATICS, 2021, 12 (2), P. 135–141
Non-compact perturbations of the spectrum of multipliers given with functions
R. R. Kucharov – National University of Uzbekistan, 100174, Tashkent, Uzbekistan; ramz3364647@yahoo.com
R. R. Khamraeva – National University of Uzbekistan, 100174, Tashkent; Westminster International University in Tashkent, 100010, 12, Istiqbol str., Tashkent, Uzbekistan; r.khamraeva@wiut.uz
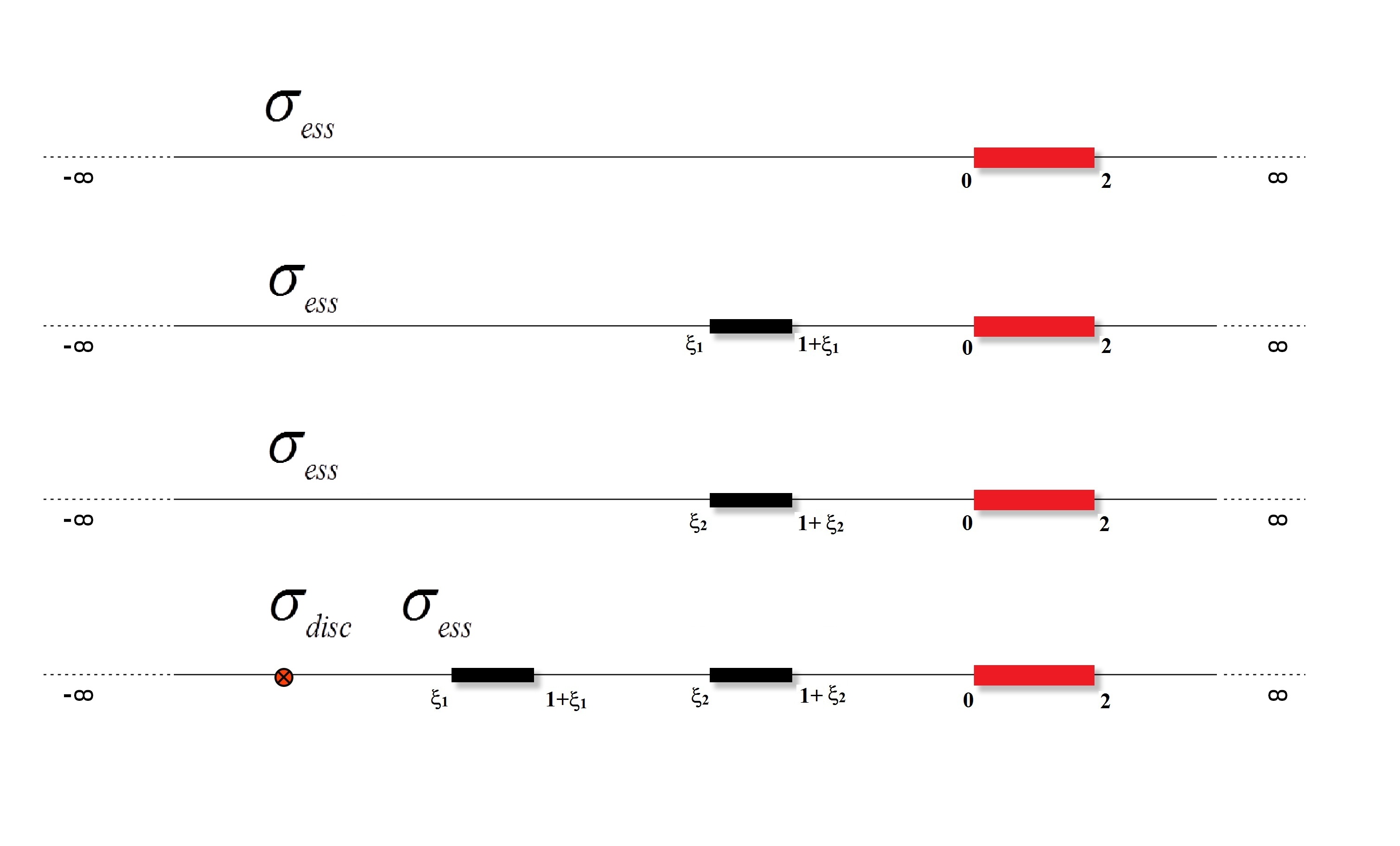
The change in the spectrum of the multipliers H0f(x; y) = xα + yβ f(x; y) and H0f(x; y) = xα yβ f(x; y) for perturbation with partial integral operators in the spaces L2[0; 1]2 is studied. Precise description of the essential spectrum and the existence of simple eigenvalue is received. We prove that the number of eigenvalues located below the lower edge of the essential spectrum in the model is finite.
Keywords: essential spectrum, discrete spectrum, lower bound of the essential spectrum, partial integral operator.
DOI 10.17586/2220-8054-2021-12-2-135-141
[In Russian] Кучаров Р.Р., Хамраева Р.Р.
Некомпактные возмущения спектра заданных мультипликаторов с функциями
Изучается изменение спектра множителей H0f(x; y) = xα + yβ f(x; y) и H0 f(x; y) = xα yβ f(x; y) при возмущении операторами в частных интегралах в пространствах L2[0; 1]2. Получено точное описание существенного спектра и существование простого собственного значения. Доказано, что число собственных значений, расположенных ниже нижнего края существенного спектра в модели, конечно.
Ключевые слова: существенный спектр, дискретный спектр, нижняя граница существенного спектра, оператор частного интеграла.