NANOSYSTEMS: PHYSICS, CHEMISTRY, MATHEMATICS, 2021, 12 (4), P. 425–429
Dirac operator with different potentials on edges of quantum graph: resonance asymptotics
A. G. Belolipetskaia – ITMO University, Kronverkskiy, 49, Saint Petersburg, 197101, Russia; annabel1502@mail.ru
I.Y. Popov – ITMO University, Kronverkskiy, 49, Saint Petersburg, 197101, Russia; popov1955@gmail.com
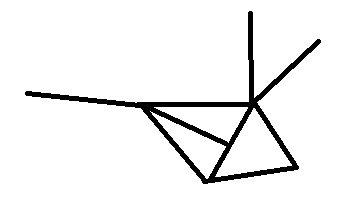
Asymptotics of resonances for the Dirac operator with different potentials on edges of a quantum graph with the Kirchhoff coupling conditions at vertices is studied. The results are obtained for a quantum graph that consists of a compact interior and a finite number of exterior edges of infinite length connected to the interior.
Keywords: quantum graph, Dirac operator, asymptotics, resonance.
DOI 10.17586/2220-8054-2021-12-4-425-429
[In Russian] А.Г. Белолипецкая, И.Ю. Попов
Оператор Дирака с различными потенциалами на ребрах квантового графа: асимптотика резонанса
Исследуется асимптотика резонансов для оператора Дирака с различными потенциалами на ребрах квантового графа с условиями связи Кирхгофа в вершинах. Результаты получены для квантового графа, состоящего из компактной внутренности и конечного числа внешних ребер бесконечной длины, соединенных с внутренностью.
Ключевые слова: квантовый граф, оператор Дирака, асимптотика, резонанс.