Nanosystems: Phys. Chem. Math., 2022, 13 (3), 245–249
Spectral gaps for star-like quantum graph and for two coupled rings
Irina V. Blinova – ITMO University, St. Petersburg, 197101, Russia;
irin-a@yandex.ru
Anton I. Popov – ITMO University, St. Petersburg, 197101, Russia; popov239@gmail.com
Anna A. Bosova – ITMO University, St. Petersburg, 197101, Russia; bossandbosss@yandex.ru
Corresponding author: I. V. Blinova, irin-a@yandex.ru
DOI 10.17586/2220-8054-2022-13-3-245-249
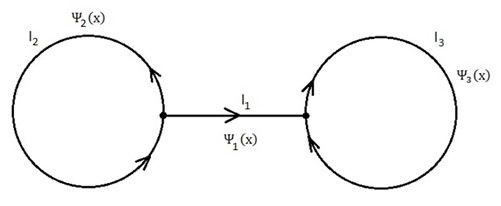
ABSTRACT The spectral problems for two types of quantum graphs are considered. We deal with star-like graph and a graph consisting of two rings connected through a segment. The spectral gap, i.e. the difference between the second and the first eigenvalues of the free Schrödinger operator, is studied. The dependence of the gap on the geometric parameters of the graph is investigated. Particularly, it is shown that the maximal gap is observed for the symmetric quantum graph.
KEYWORDS spectral gap, quantum graph, Schrödinger operator, discrete spectrum.
FOR CITATION Blinova I.V., Popov A.I., Bosova A.A. Spectral gaps for star-like quantum graph and for two coupled rings. Nanosystems: Phys. Chem. Math., 2022, 13 (3), 245–249.
[In Russian] И.В. Блинова, А.И. Попов, А.А. Босова
Спектральная лакуна для звездного квантового графа и для двух связанных колец
АННОТАЦИЯ Рассмотрены спектральные задачи для двух типов квантовых графов. Мы имеем дело со звездообразным графом и графом, состоящим из двух колец, соединенных отрезком. Исследуется спектральная лакуна, т.е. разность между вторым и первым собственными значениями свободного оператора Шредингера. Исследована зависимость лакуны от геометрических параметров графа. В частности, показано, что максимальный разрыв наблюдается для симметричного квантового графа.
КЛЮЧЕВЫЕ СЛОВА спектральная лакуна, квантовый граф, оператор Шредингера, дискретный спектр.