Nanosystems: Phys. Chem. Math., 2024, 15 (1), 23–30
On solutions to nonlinear integral equation of the Hammerstein type and its applications to Gibbs measures for continuous spin systems
Ismoil M. Mavlonov – National University of Uzbekistan, Tashkent, Uzbekistan; mavlonovismoil16@gmail.com
Aloberdi M. Sattarov – University of Business and Science, Namangan, Uzbekistan; saloberdi90@mail.ru
Sevinchbonu A. Karimova – National University of Uzbekistan, Tashkent, Uzbekistan
Farhod H. Haydarov – Institute of Mathematics, Tashkent; New Uzbekistan University, Tashkent; National University of Uzbekistan, Tashkent, Uzbekistan; haydarov_imc@mail.ru
Corresponding author: I. M. Mavlonov, mavlonovismoil16@gmail.com
DOI 10.17586/2220-8054-2024-15-1-23-30
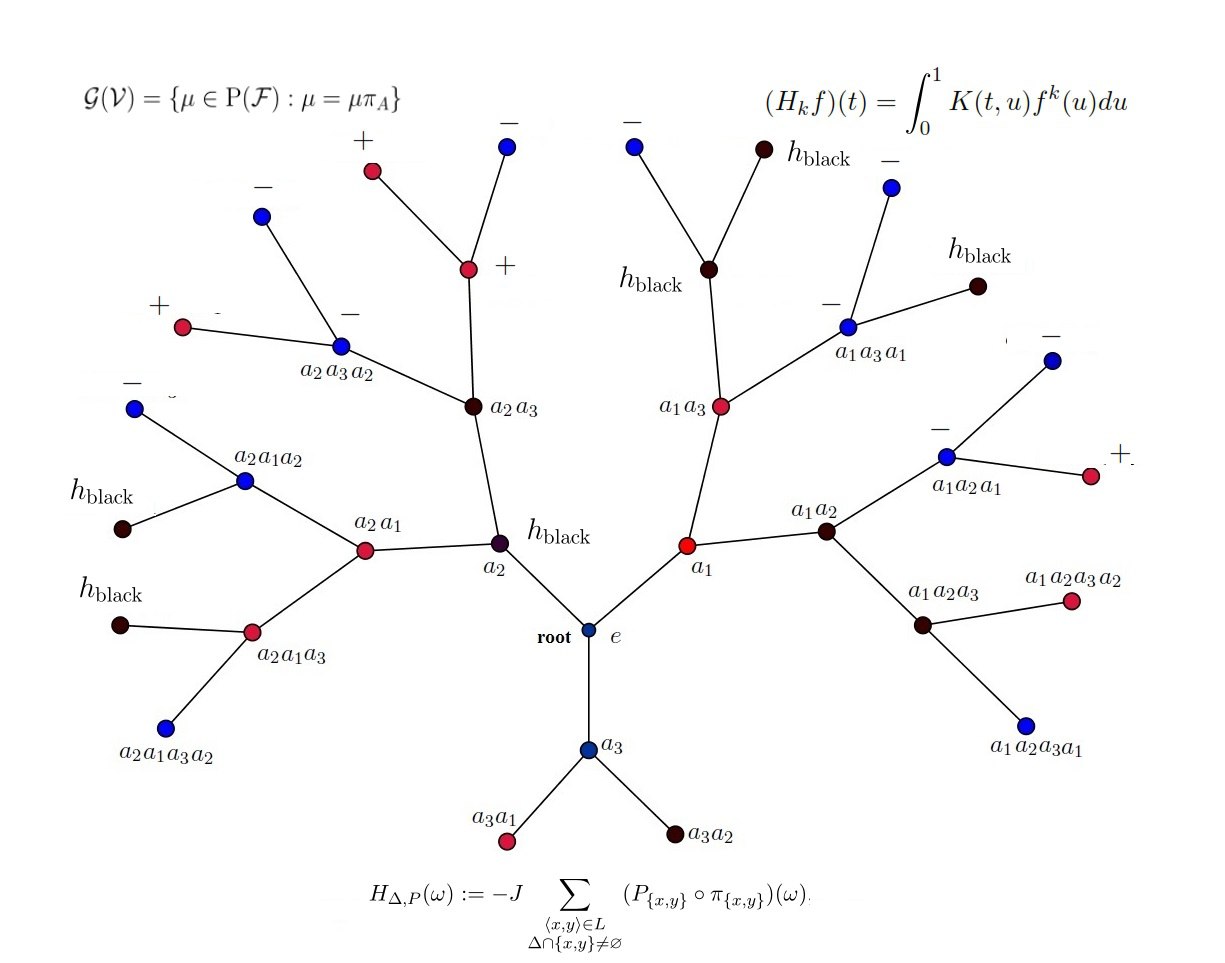
ABSTRACT The paper deals with the problem of constructing kernels of Hammerstein-type equations whose positive solutions are not unique. This problem arises from the theory of Gibbs measures, and each positive solution of the equation corresponds to one translation-invariant Gibbs measure. Also, the problem of finding kernels for which the number of positive solutions to the equation is greater than one is equivalent to the problem of finding models which has phase transition. In these articles, the number of solutions corresponding to the constructed kernels does not exceed 3, and in turn, it only gives us a chance to check the existence of phase transitions. The constructed kernels in this paper are more general than the kernels in the abovementioned papers and except for checking phase transitions, it allows us to classify the set of Gibbs measures.
KEYWORDS Generalized SOS model, spin values, Cayley tree, gradient Gibbs measure, periodic boundary law
ACKNOWLEDGEMENTS We thank the referee for careful reading of the manuscript; in particular, for some comments, useful discussions, and suggestions which have improved the paper.
FOR CITATION Mavlonov I.M., Sattarov A.M., Karimova S.A., Haydarov F.H. On solutions to nonlinear integral equation of the Hammerstein type and its applications to Gibbs measures for continuous spin systems. Nanosystems: Phys. Chem. Math., 2024, 15 (1), 23–30.
[In Russian] И. М. Мавлонов, А. М. Саттаров, С. А. Каримова, Ф. Х. Хайдаров
О решениях нелинейного интегрального уравнения тип Хаммерштейна и его приложения к мерам гиббса длянепрерывной спиновой системы
АННОТАЦИЯ В данной работе рассматривается проблема построения ядер уравнений типа Хаммерштейна, чьи положительные решения не являются уникальными. Эта проблема возникает из теории мер Гиббса, и каждое положительное решение уравнения соответствует одной трансляционно-инвариантной мере Гиббса. Кроме того, проблема поиска ядер, для которых количество положительных решений уравнения превышает одно, эквивалентна проблеме поиска моделей с фазовым переходом. Проблема построения ядер уравнения, для которых есть как минимум два положительных решения, также изучается в [1, 4, 12, 13, 15]. В этих статьях количество решений, соответствующих построенным ядрам, не превышает 3, и в свою очередь, это дает нам возможность проверить наличие фазовых переходов. Построенные в данной статье ядра более общие, чем ядра в упомянутых выше работах, и помимо проверки фазовых переходов, они позволяют классифицировать множество мер Гиббса.
КЛЮЧЕВЫЕ СЛОВА Обобщенная модель SOS, спиновые значения, дерево Кэли, градиентная мера Гиббса, периодическое граничное условие.