Nanosystems: Phys. Chem. Math., 2024, 15 (5), 567–575
Eccentricity Laplacian energy of a graph
A. Harshitha – Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal, India, 576104; harshuarao@gmail.com
S. Nayak – Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal, India, 576104; swati.nayak@manipal.edu
S. D’Souza – Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal, India, 576104; sabitha.dsouza@manipal.edu
Corresponding author: S. D’Souza, sabitha.dsouza@manipal.edu
DOI 10.17586/2220-8054-2024-15-5-567-575
PACS 05C50.90E10
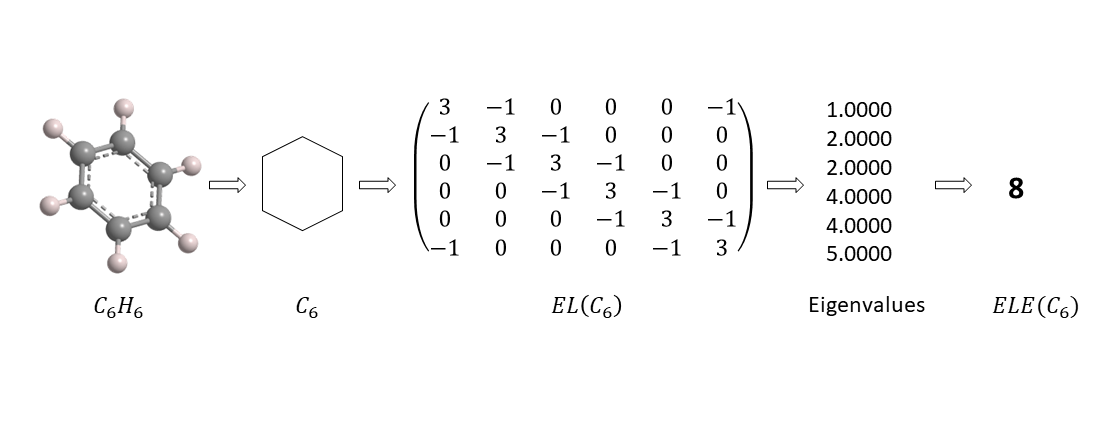
ABSTRACT Let G be a simple, finite, undirected and connected graph. The eccentricity of a vertex v is the maximum distance from v to all other vertices of G. The eccentricity Laplacian matrix of G with n vertices is a square matrix of order n, whose elements are elij , where elij is −1 if the corresponding vertices are adjacent, elij is the eccentricity of vi for 1 ≤ i ≤ n, and elij is 0 otherwise. If ε1, ε2, . . . , εn are the eigenvalues of the eccentricity Laplacian matrix, then the eccentricity Laplacian energy of G is ELE(G) = Σ |εi − avec(G)|, where avec(G) is the average eccentricities of all the vertices of G. In this study, some properties of the eccentricity Laplacian energy are obtained and comparison between thge eccentricity Laplacian energy and the total π−electron energy is obtained.
KEYWORDS distance, eccentricity, Laplacian energy
FOR CITATION Harshitha A., Nayak S., D’Souza S. Eccentricity Laplacian energy of a graph. Nanosystems: Phys. Chem. Math., 2024, 15 (5), 567–575.
[In Russian] А.Харшита, С. Наяк, С. Д’Соуза
Эксцентричность лапласиана энергии графа
АННОТАЦИЯ Пусть G – простой конечный неориентированный связный граф. Эксцентричность вершины v есть максимальное расстояние от v до всех остальных вершин графа G. Матрица эксцентричности лапласиана графа G с n вершинами – это квадратная матрица порядка n, элементы которой elij, где elij есть -1, если соответствующие вершины соседние, elij есть эксцентричность вершины vi для I от 1 до n, elij есть 0 в остальных случаях. Если ε1, ε2, . . . , εn – собственные значения матрицы эксцентричности лапласиана энергии, то эксцентричность лапласиана энергии G есть ELE(G) = Σ |εi − avec(G)|, где avec(G) средняя эксцентричность всех вершин G. В данном исследовании получены некоторые свойства эксцентричности лапласиана энергии и проведено сравнение между эксцентричностью лапласиана энергии и полной энергией π-электронов.
КЛЮЧЕВЫЕ СЛОВА расстояние, эксцентричность, лапласиан энергии