Nanosystems: Phys. Chem. Math., 2024, 15 (6), 736–741
Boundary composed of small Helmholtz resonators: asymptotic approach
Igor Y. Popov – ITMO University, St. Petersburg, Russia; popov1955@gmail.com
Ekaterina S. Trifanova – ITMO University, St. Petersburg, Russia; etrifanova@gmail.com
Alexander S. Bagmutov – ITMO University, St. Petersburg, Russia; bagmutov94@mail.ru
Alexander A. Lytaev – ITMO University, St. Petersburg; Institute for Problems in Mechanical Engineering of the Russian Academy of Sciences, St. Petersburg, Russia; sas-lyt@ya.ru
Corresponding author: I. Y. Popov, popov1955@gmail.com
DOI 10.17586/2220-8054-2024-15-6-736-741
PACS 73.23.Ra, 73.63.Nm
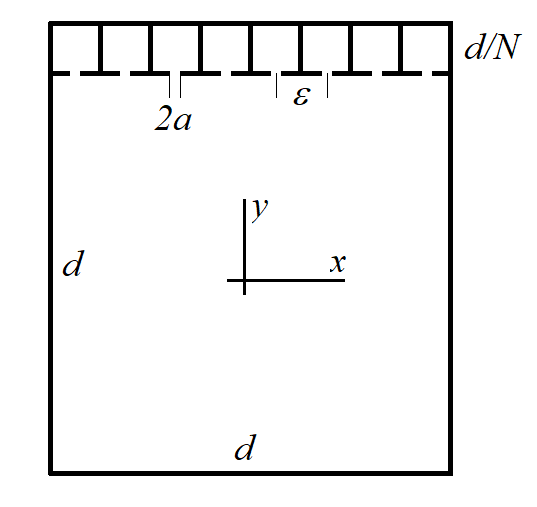
ABSTRACT We consider the solution of the two-dimensional Neumann problem for the Helmholtz equation in a complex region composed of a square resonator with large number of smaller square resonators connected to it through small apertures along one side. The sizes of the apertures and distances between the neighbour apertures tend to zero. We use the method of matching of asymptotic expansions of solutions. By directing the number of attached small resonators to infinity, we obtain a problem for the Laplacian in the main square with energy-dependent boundary condition.
KEYWORDS eigenfunction, Helmholtz equation, boundary problem, asymptotics
ACKNOWLEDGEMENTS This work was partially financially supported by Russian Science Foundation (grant 24-21-00107, https://rscf.ru/en/project/24-21-00107/).
FOR CITATION Popov I.Y., Trifanova E.S., Bagmutov A.S., Lytaev A.A. Boundary composed of small Helmholtz resonators: asymptotic approach. Nanosystems: Phys. Chem. Math., 2024, 15 (6), 736–741.
[In Russian] И.Ю. Попов, Е.С. Трифанова, А.С. Багмутов, А.А. Лытаев
Граница, состоящая из малых резонаторов Гельмгольца: асимптотический подход
АННОТАЦИЯ Мы рассматриваем решение двумерной задачи Неймана для уравнения Гельмгольца в сложной области, состоящей из квадратного резонатора с большим количеством меньших квадратных резонаторов, присоединенных к нему через малые отверстия вдоль одной стороны. Размеры отверстий и расстояния между соседними отверстиями стремятся к нулю. Мы используем метод согласования асимптотических разложений решений. Устремляя число присоединенных малых резонаторов к бесконечности, мы получаем задачу для оператора Лапласа в главном квадрате с граничным условием, зависящим от энергии.
КЛЮЧЕВЫЕ СЛОВА собственная функция, уравнение Гельмгольца, краевая задача, асимптотика