Nanosystems: Phys. Chem. Math., 2024, 15 (6), 742–748
Qualitative properties of the mathematical model of nonlinear cross-diffusion processes
Sokhibjan Muminov – Mamun university, Khiva; Urgench state university, Urgench, Uzbekistan; sokhibjan.muminov@mamunedu.uz
Praveen Agarwal – Nonlinear Dynamics Research Center (NDRC), Ajman University, Ajman, UAE; Anand International College of Engineering, Jaipur; International Center for Basic and Applied Sciences, Jaipur, India; praveen.agarwal@anandice.ac.in
Dildora Muhamediyeva – Tashkent University of information technologies named after Muhammad Al-Khwarizmi, Tashkent, Uzbekistan; matematichka@inbox.ru
Corresponding author: S. Muminov, sokhibjan.muminov@mamunedu.uz
DOI 10.17586/2220-8054-2024-15-6-742-748
PACS 35A01, 35B44, 35K57, 35K65
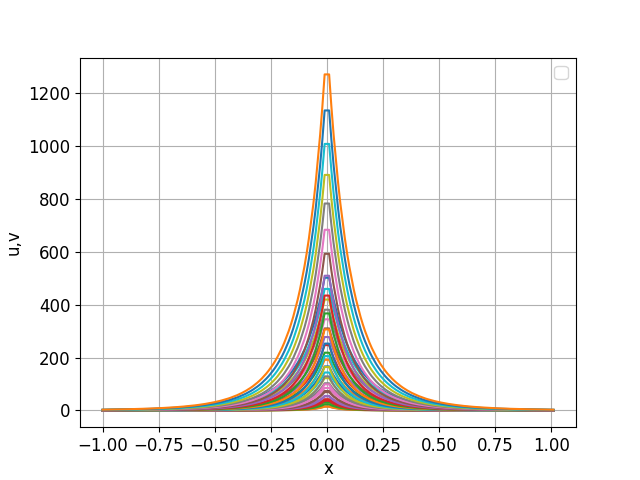
ABSTRACT The work is devoted to developing a self-similar solution for a system of nonlinear differential equations that describe diffusion processes. Various techniques are used to examine the capacity for generating self-similar solutions that can estimate and predict system behavior under diffusion conditions. The focus is on developing and applying numerical algorithms, as well as using theoretical tools such as asymptotic analysis, to obtain more accurate and reliable results. The study’s results can be applied to various scientific and technical fields, such as physics, chemistry, biology, and engineering, where diffusion processes play an essential role. The development of self-similar solutions for systems of nonlinear differential equations related to diffusion opens novel opportunities for modeling and analyzing complex systems and enhancing diffusion
processes in various fields.
KEYWORDS nonlinear system, diffusion, self-similar solution, flow, model, algorithm, parabolic differential equation.
FOR CITATION Muminov S., Agarwal P., Muhamediyeva D. Qualitative properties of the mathematical model of nonlinear cross-diffusion processes. Nanosystems: Phys. Chem. Math., 2024, 15 (6), 742–748.
[In Russian] С. Муминов, П. Агарвал, Д. Мухамедиева
Качественные свойства математической модели нелинейных кросс-диффузионных процессов
АННОТАЦИЯ Работа посвящена разработке самоподобного решения для системы нелинейных дифференциальных уравнений, описывающих процессы диффузии. Различные методы используются для изучения возможности генерации самоподобных решений, которые могут оценивать и предсказывать поведение системы в условиях диффузии. Основное внимание уделяется разработке и применению численных алгоритмов, а также использованию теоретических инструментов, таких как асимптотический анализ, для получения более точных и надежных результатов. Результаты исследования могут быть применены в различных научных и технических областях, таких как физика, химия, биология и инженерия, где процессы диффузии играют существенную роль. Разработка самоподобных решений для систем нелинейных дифференциальных уравнений, связанных с диффузией, открывает новые возможности для моделирования и анализа сложных систем и улучшения процессов диффузии в различных областях.
КЛЮЧЕВЫЕ СЛОВА нелинейная система, диффузия, автомодельное решение, поток, модель, алгоритм, параболическое дифференциальное уравнение.