Nanosystems: Phys. Chem. Math., 2024, 15 (6), 749–754
Some conditions for the existence of 4-periodic solutions in non-homogeneous differential equations involving piecewise alternately advanced and retarded arguments
Kuo-Shou Chiu – Departamento de Matemática, Facultad de Ciencias Básicas, Universidad Metropolitana de Ciencias de la Educación, José Pedro Alessandri 774, Santiago, Chile; kschiu@umce.cl
Fernando Cordova-Lepe – Departamento de Matemática, Física y Estadística, Universidad Católica del Maule, Talca, Chile
Corresponding author: Kuo-Shou Chiu, kschiu@umce.cl
DOI 10.17586/2220-8054-2024-15-6-749-754
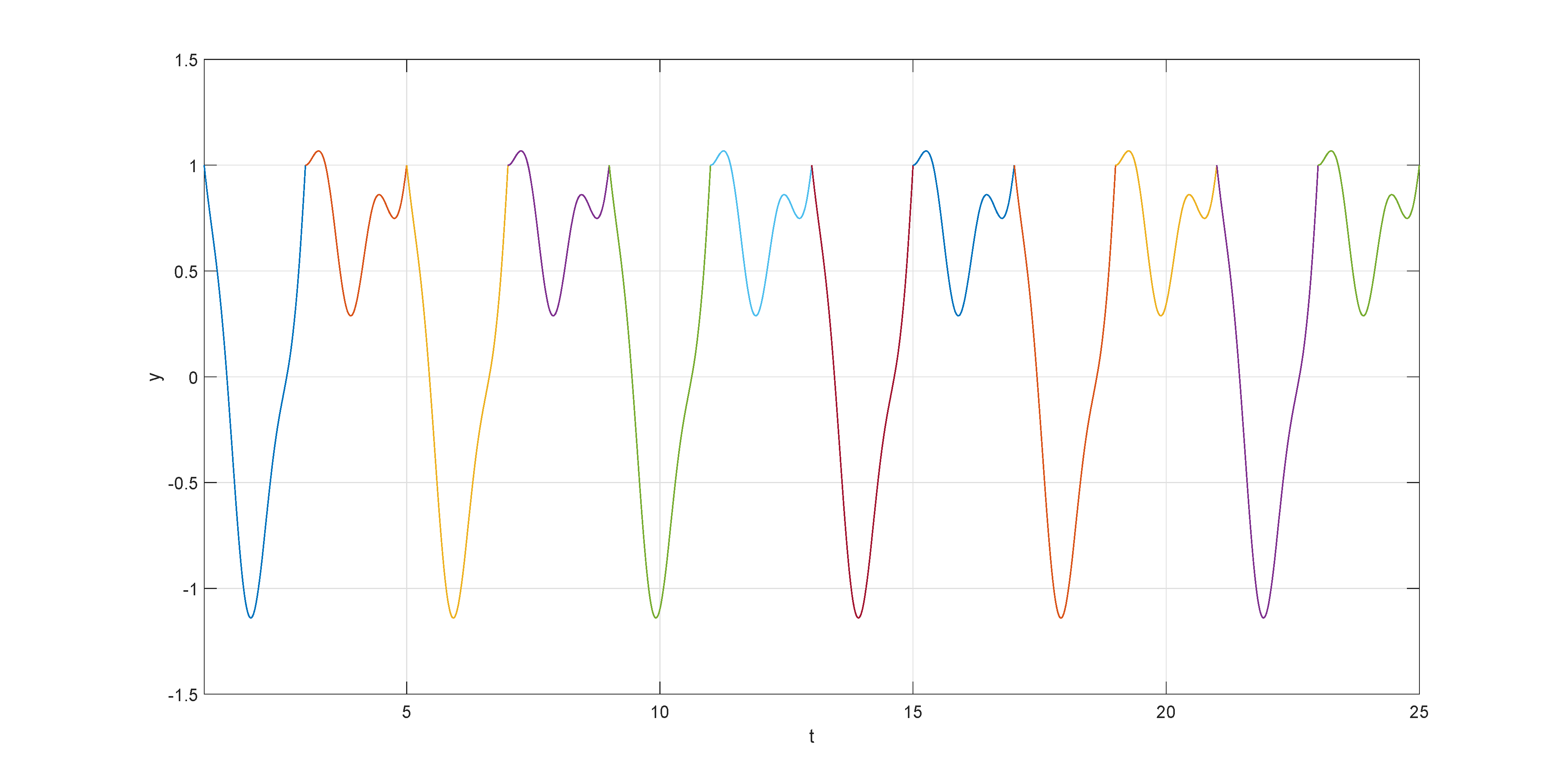
ABSTRACT The manuscript introduces a method to characterize 4-periodic solutions in first-order non-homogeneous differential equations involving piecewise alternately advanced and retarded argument. It systematically delineates the prerequisites for these solutions to exist and furnishes precise methodologies for their determination. Additionally, the paper includes the illustrative example, including scenarios with infinitely many solutions, to demonstrate the effectiveness of the proposed approach.
KEYWORDS Piecewise alternately advanced and retarded argument, Periodic solution
ACKNOWLEDGEMENTS This research was in part supported by ANID FONDECYT Nº 1231256 and DIUMCE 09-2023-SAC.
FOR CITATION Kuo-Shou Chiu, Fernando Cordova-Lepe Some conditions for the existence of 4-periodic solutions in non-homogeneous differential equations involving piecewise alternately advanced and retarded arguments. Nanosystems: Phys. Chem. Math., 2024, 15 (6), 749–754.
[In Russian] Куо-Шоу Чиу, Фернандо Кордова-Лепе
Некоторые условия существования 4-периодических решений в неоднородных дифференциальных уравнениях с кусочно-попеременно опережающими и запаздывающими аргументами
АННОТАЦИЯ В рукописи представлен метод характеризации 4-периодических решений в неоднородных дифференциальных уравнениях первого порядка, включающих кусочно-попеременно опережающий и запаздывающий аргумент. Он систематически описывает предпосылки для существования этих решений и предоставляет точные методологии для их определения. Кроме того, в статью включен иллюстративный пример, включая сценарии с бесконечным количеством решений, для демонстрации эффективности предлагаемого подхода.
КЛЮЧЕВЫЕ СЛОВА Кусочно-попеременно опережающий и запаздывающий аргумент, Периодическое решение.