NANOSYSTEMS: PHYSICS, CHEMISTRY, MATHEMATICS, 2017, 8 (3), P. 317–322
To the qualitative properties of solution of system equations not in divergence form of polytrophic filtration in variable density
M. Aripov – National University of Uzbekistan, Applied Mathematics and Computer Analysis, Universitet, 4, Tashkent, 100174, Uzbekistan; mirsaidaripov@mail.ru
A. S. Matyakubov – National University of Uzbekistan, Applied Mathematics and Computer Analysis, Universitet, 4, Tashkent, 100174, Uzbekistan; almasa@list.ru
In this paper, the properties of solutions for the nonlinear system equations not in divergence form:
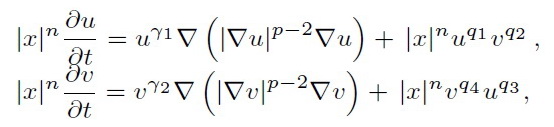
are studied. In this work, we used method of nonlinear splitting, known previously for nonlinear parabolic equations, and systems of equations in divergence form, asymptotic theory and asymptotic methods based on different transformations. Asymptotic representation of self-similar solutions for the nonlinear parabolic system of equations not in divergence form is constructed. The property of finite speed propagation of distributions (FSPD) and the asymptotic behavior of the weak solutions were studied for the slow diffusive case.
Keywords: nonlinear system of equations, not in divergence form, global solutions, self-similar solutions, asymptotic representation of solution.
PACS 02.30.Jr, 02.30.Mv, 11.10.Jj, 11.10.Lm
DOI 10.17586/2220-8054-2017-8-3-317-322